Icosahedron Class Documentation
Overview
References
- Wikipedia | Icosahedron
- Wikipedia | Regular Icosahedron
- Wolfram Mathworld | Icosahedron
- Wolfram Mathworld | Regular Icosahedron
Class Documentation
Bases: Polyhedron
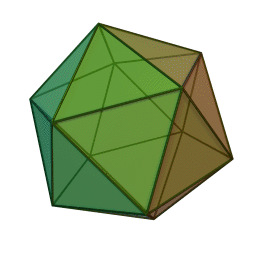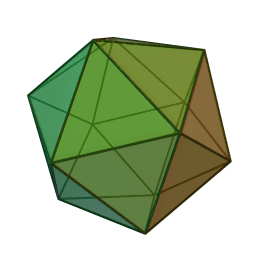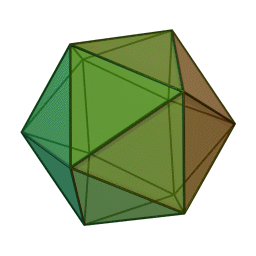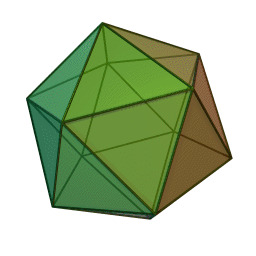
Icosahedron Class
Regular unit icosahedron.
calc_angle_dihedral()
staticmethod
Face-edge-face angle, i.e., "dihedral angle" (approx. 138.190)
calc_angle_solid_vertex()
staticmethod
Solid angle at a vertex subtended by a face (approx. 2.63455 steradians)
calc_angle_subtended(a)
staticmethod
Vertex-Center-Vertex angle calc_face_angle_face_edge_face The angle between lines from the dodecahedron center to any two vertices. It is also the angle between Plateau borders at a vertex. In chemistry it is called the tetrahedral bond angle. This angle (in radians) is also the length of the circular arc on the unit sphere resulting from centrally projecting one edge of the dodecahedron to the sphere.
(approx. 63.435)
calc_area(a)
staticmethod
Formula to calculate area of Icosahedron
calc_radius_circumsphere(a)
staticmethod
Radius of circumsphere the radius of a circumscribed sphere (one that touches the icosahedron at all vertices)
~ 0.9510565163 * a
calc_radius_insphere(a)
staticmethod
Radius of insphere that is tangent to faces The radius of an inscribed sphere (tangent to each of the icosahedron's faces) is
~ 0.7557613141 * a
calc_radius_midsphere(a)
staticmethod
Radius of midsphere that is tangent to edges
while the midradius, which touches the middle of each edge, is
calc_volume(a)
staticmethod
Formula to calculate volume of Icosahedron
faces()
staticmethod
20 faces
vertices()
staticmethod
12 principal directions in 3D space: points on an unit Icosahedron.
Vertex coordinates:
Position 1 ( 0, ±1, ±φ) (±1, ±φ, 0) (±φ, 0, ±1)
or:
Position 2 ( 0, ±φ, ±1) (±φ, ±1, 0) (±1, 0, ±φ)